The Hill Cipher was invented by Lester S. Hill in 1929, and like the other Digraphic Ciphers it acts on groups of letters. Unlike the others though it is extendable to work on different sized blocks of letters. So, technically it is a polygraphic substitution cipher, as it can work on digraphs, trigraphs (3 letter blocks) or theoretically any sized blocks.
The Hill Cipher uses an area of mathematics called Linear Algebra, and in particular requires the user to have an elementary understanding of matrices. It also make use of Modulo Arithmetic (like the Affine Cipher). Because of this, the cipher has a significantly more mathematical nature than some of the others. However, it is this nature that allows it to act (relatively) easily on larger blocks of letters.
In the examples given, we shall walk through all the steps to use this cipher to act on digraphs and trigraphs. It can be extended further, but this then requires a much deeper knowledge of the background mathematics. Some important concepts are used throughout: Matrix Multiplication; Modular Inverses; Determinants of Matrices; Matrix Adjugates (for finding inverses).
Encryption
To encrypt a message using the Hill Cipher we must first turn our keyword into a key matrix (a 2 x 2 matrix for working with digraphs, a 3 x 3 matrix for working with trigraphs, etc). We also turn the plaintext into digraphs (or trigraphs) and each of these into a column vector. We then perform matrix multiplication modulo the length of the alphabet (i.e. 26) on each vector. These vectors are then converted back into letters to produce the ciphertext.
2 x 2 Example
We shall encrypt the plaintext message "short example" using the keyword hill and a 2 x 2 matrix. The first step is to turn the keyword into a matrix. If the keyword was longer than the 4 letters needed, we would only take the first 4 letters, and if it was shorter, we would fill it up with the alphabet in order (much like a Mixed Alphabet).
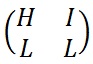
The keyword written as a matrix.
With the keyword in a matrix, we need to convert this into a key matrix. We do this by converting each letter into a number by its position in the alphabet (starting at 0). So, A = 0, B = 1, C= 2, D = 3, etc.
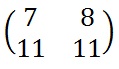
The key matrix (each letter of the keyword is converted to a number).
We now split the plaintext into digraphs, and write these as column vectors. That is, in the first column vector we write the first plaintext letter at the top, and the second letter at the bottom. Then we move to the next column vector, where the third plaintext letter goes at the top, and the fourth at the bottom. This continues for the whole plaintext.
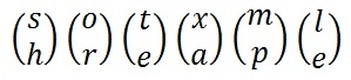
The plaintext "short example" split into column vectors.
Now we must convert the plaintext column vectors in the same way that we converted the keyword into the key matrix. Each letter is replaced by its appropriate number.
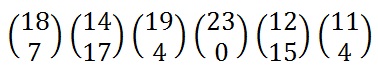
The plaintext converted into numeric column vectors.
Now we must perform some matrix multiplication. We multiply the key matrix by each column vector in turn. We shall go through the first of these in detail, then the rest shall be presented in less detail. We write the key matrix first, followed by the column vector.
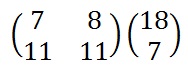
To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the bottom row of the key matrix with the column vector to get the bottom element of the resulting column vector. The way we "combine" the four numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, and multiply the second element of the key matrix row by the bottom element of the column vector. We then add together these two answers.
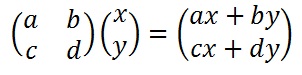
The algebraic rules of matrix multiplication.
That is, we follow the rules given by the algebraic method shown to the left.
In our case we perform the two calculations on the right. We then right these two answers out in a column vector as shown below.
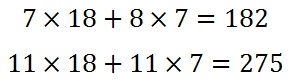
The calculations performed when doing a matrix multiplication.
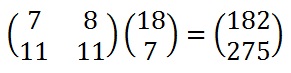
The shorthand for the matrix multiplication.
Next we have to take each of these numbers, in our resultant column vector, modulo 26 (remember that means divide by 26 and take the remainder).
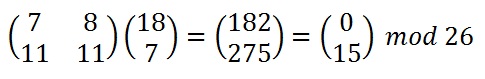
Reducing the resultant column vector modulo 26.
Finally we have to convert these numbers back to letters, so 0 becomes "A" and 15 becomes "P", and our first two letters of the ciphertext are "AP".
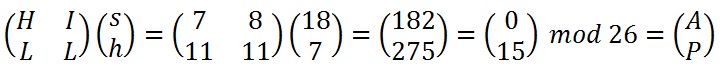
The whole calculation: converting to numbers; the matrix multiplication; reducing modulo 26; converting back to letters.
3 x 3 Example
We shall encrypt the plaintext message "retreat now" using the keyphrase back up and a 3 x 3 matrix. The first step is to turn the key phrase into a matrix. Notice that the key phrase is a few letters short, so we fill in the final elements with the start of the alphabet.

The keyword written as a matrix.
Now we turn the keyword matrix into the key matrix by replacing letters with their numeric values.
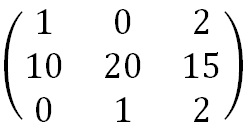
The Key Matrix obtained by taking the numeric values of the letters of the key phrase.
Now we split the plaintext into trigraphs (we are using a 3 x 3 matrix so we need groups of 3 letters), and convert these into column vectors. However, since the plaintext does not go perfectly into the column vectors, we need to use some nulls to make the plaintext the right length. We then convert these into numeric column vectors.
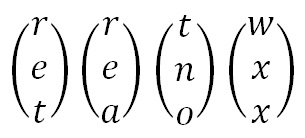
The plaintext split into trigraphs and written in column vectors. Note the nulls added to make it the right length
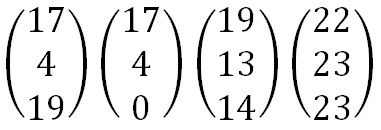
The plaintext converted into numeric column vectors.
Now we perform matrix multiplication, multiplying the key matrix by each column vector in turn. To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the middle row of the key matrix with the column vector to get the middle element of the resulting column vector. and similarly for the bottom row. The way we "combine" the six numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, multiply the second element of the key matrix row by the middle element of the column vector, and multiply the third element of the key matrix row by the bottom element of the column vector. We then add together these three answers.
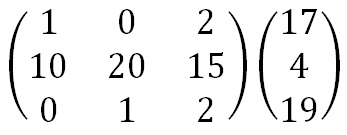
The first matrix mltiplication.
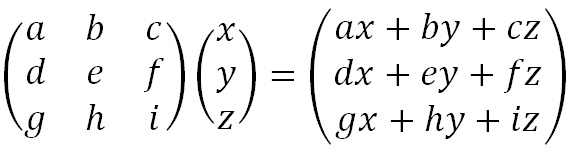
Algebraic representation of matrix multiplication for a 3 x 3 matrix.
We then follow the same process as for the 2 x 2 Matrix Example. We perform all the matrix multiplcations, and take the column vectors modulo 26. Then we convert them back into letters to produce the ciphertext.
The Hill Cipher uses an area of mathematics called Linear Algebra, and in particular requires the user to have an elementary understanding of matrices. It also make use of Modulo Arithmetic (like the Affine Cipher). Because of this, the cipher has a significantly more mathematical nature than some of the others. However, it is this nature that allows it to act (relatively) easily on larger blocks of letters.
In the examples given, we shall walk through all the steps to use this cipher to act on digraphs and trigraphs. It can be extended further, but this then requires a much deeper knowledge of the background mathematics. Some important concepts are used throughout: Matrix Multiplication; Modular Inverses; Determinants of Matrices; Matrix Adjugates (for finding inverses).
Encryption
To encrypt a message using the Hill Cipher we must first turn our keyword into a key matrix (a 2 x 2 matrix for working with digraphs, a 3 x 3 matrix for working with trigraphs, etc). We also turn the plaintext into digraphs (or trigraphs) and each of these into a column vector. We then perform matrix multiplication modulo the length of the alphabet (i.e. 26) on each vector. These vectors are then converted back into letters to produce the ciphertext.
2 x 2 Example
We shall encrypt the plaintext message "short example" using the keyword hill and a 2 x 2 matrix. The first step is to turn the keyword into a matrix. If the keyword was longer than the 4 letters needed, we would only take the first 4 letters, and if it was shorter, we would fill it up with the alphabet in order (much like a Mixed Alphabet).
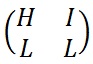
The keyword written as a matrix.
With the keyword in a matrix, we need to convert this into a key matrix. We do this by converting each letter into a number by its position in the alphabet (starting at 0). So, A = 0, B = 1, C= 2, D = 3, etc.
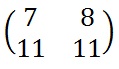
The key matrix (each letter of the keyword is converted to a number).
We now split the plaintext into digraphs, and write these as column vectors. That is, in the first column vector we write the first plaintext letter at the top, and the second letter at the bottom. Then we move to the next column vector, where the third plaintext letter goes at the top, and the fourth at the bottom. This continues for the whole plaintext.
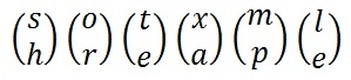
The plaintext "short example" split into column vectors.
Now we must convert the plaintext column vectors in the same way that we converted the keyword into the key matrix. Each letter is replaced by its appropriate number.
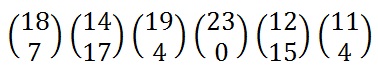
The plaintext converted into numeric column vectors.
Now we must perform some matrix multiplication. We multiply the key matrix by each column vector in turn. We shall go through the first of these in detail, then the rest shall be presented in less detail. We write the key matrix first, followed by the column vector.
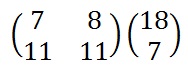
To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the bottom row of the key matrix with the column vector to get the bottom element of the resulting column vector. The way we "combine" the four numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, and multiply the second element of the key matrix row by the bottom element of the column vector. We then add together these two answers.
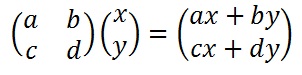
The algebraic rules of matrix multiplication.
That is, we follow the rules given by the algebraic method shown to the left.
In our case we perform the two calculations on the right. We then right these two answers out in a column vector as shown below.
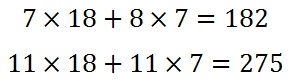
The calculations performed when doing a matrix multiplication.
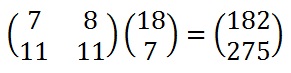
The shorthand for the matrix multiplication.
Next we have to take each of these numbers, in our resultant column vector, modulo 26 (remember that means divide by 26 and take the remainder).
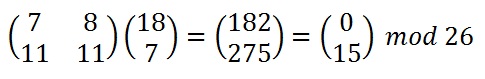
Reducing the resultant column vector modulo 26.
Finally we have to convert these numbers back to letters, so 0 becomes "A" and 15 becomes "P", and our first two letters of the ciphertext are "AP".
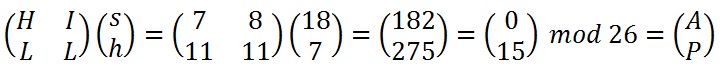
The whole calculation: converting to numbers; the matrix multiplication; reducing modulo 26; converting back to letters.
3 x 3 Example
We shall encrypt the plaintext message "retreat now" using the keyphrase back up and a 3 x 3 matrix. The first step is to turn the key phrase into a matrix. Notice that the key phrase is a few letters short, so we fill in the final elements with the start of the alphabet.

The keyword written as a matrix.
Now we turn the keyword matrix into the key matrix by replacing letters with their numeric values.
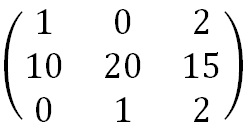
The Key Matrix obtained by taking the numeric values of the letters of the key phrase.
Now we split the plaintext into trigraphs (we are using a 3 x 3 matrix so we need groups of 3 letters), and convert these into column vectors. However, since the plaintext does not go perfectly into the column vectors, we need to use some nulls to make the plaintext the right length. We then convert these into numeric column vectors.
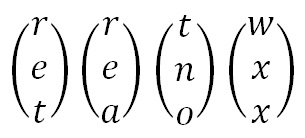
The plaintext split into trigraphs and written in column vectors. Note the nulls added to make it the right length
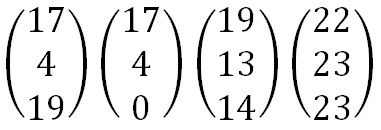
The plaintext converted into numeric column vectors.
Now we perform matrix multiplication, multiplying the key matrix by each column vector in turn. To perform matrix multiplication we "combine" the top row of the key matrix with the column vector to get the top element of the resulting column vector. We then "combine" the middle row of the key matrix with the column vector to get the middle element of the resulting column vector. and similarly for the bottom row. The way we "combine" the six numbers to get a single number is that we multiply the first element of the key matrix row by the top element of the column vector, multiply the second element of the key matrix row by the middle element of the column vector, and multiply the third element of the key matrix row by the bottom element of the column vector. We then add together these three answers.
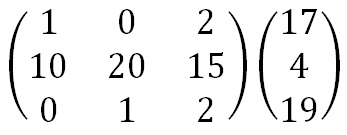
The first matrix mltiplication.
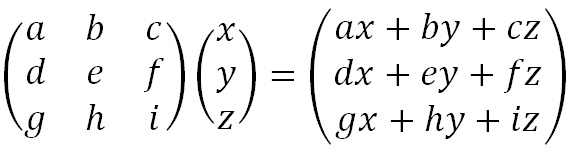
Algebraic representation of matrix multiplication for a 3 x 3 matrix.
We then follow the same process as for the 2 x 2 Matrix Example. We perform all the matrix multiplcations, and take the column vectors modulo 26. Then we convert them back into letters to produce the ciphertext.
Security[edit]
The basic Hill cipher is vulnerable to a known-plaintext attack because it is completely linear. An opponent who intercepts plaintext/ciphertext character pairs can set up a linear system which can (usually) be easily solved; if it happens that this system is indeterminate, it is only necessary to add a few more plaintext/ciphertext pairs. Calculating this solution by standard linear algebra algorithms then takes very little time.While matrix multiplication alone does not result in a secure cipher it is still a useful step when combined with other non-linear operations, because matrix multiplication can provide diffusion. For example, an appropriately chosen matrix can guarantee that small differences before the matrix multiplication will result in large differences after the matrix multiplication. Indeed, some modern ciphers use a matrix multiplication step to provide diffusion. For example, the MixColumns step in AES is a matrix multiplication. The function gin Twofish is a combination of non-linear S-boxes with a carefully chosen matrix multiplication (MDS).Mechanical implementation[edit]
When operating on 2 symbols at once, a Hill cipher offers no particular advantage over Playfair or the bifid cipher, and in fact is weaker than either, and slightly more laborious to operate by pencil-and-paper. As the dimension increases, the cipher rapidly becomes infeasible for a human to operate by hand.A Hill cipher of dimension 6 was implemented mechanically. Hill and a partner were awarded a patent (U.S. Patent 1,845,947) for this device, which performed a 6 × 6 matrix multiplication modulo 26 using a system of gears and chains.Unfortunately the gearing arrangements (and thus the key) were fixed for any given machine, so triple encryption was recommended for security: a secret nonlinear step, followed by the wide diffusive step from the machine, followed by a third secret nonlinear step. (The much later Even-Mansour cipher also uses an unkeyed diffusive middle step). Such a combination was actually very powerful for 1929, and indicates that Hill apparently understood the concepts of a meet-in-the-middle attack as well as confusion and diffusion. Unfortunately, his machine did not sell.Follow me and check how to build a strong profile digitally
---------------------------------------------------------------------------



